BECE 2015: Chief Examiner's Report for Mathematics
WAEC Chief Examiner's Report on Mathematics was as follows:
MATHEMATICS 2
1. GENERAL COMMENTS
The standard of the paper compared with those of the previous years. The performance of candidates was quite encouraging.
2. SUMMARY OF CANDIDATES' STRENGTHS
The Chief Examiner listed some of the strengths of candidates as ability to:
(i) draw a Venn diagram and labelling the sets involved,
(ii) solving inequalities,
(iii) converting mixed numbers into improper fractions in order to simplify
algebraic expressions.
(iv) constructing a triangle to given dimensions
3. SUMMARY OF CANDIDATES' WEAKNESSES
Candidates' weaknesses were shown in areas such as:
(i) representing number of elements in a set on the Venn diagram
(ii) solving word problems involving fractions,
(iii) understanding of the phrase ''how many''
(iv) determining the rule of a mapping,
(v) distinguishing between the total surface area of a closed cylinder and a cylinder closed at one end.
4. SUGGESTED REMEDIES
(i) Students should be given proper tuition in areas of weaknesses.
(ii) adequate exercise should be given to candidates to eliminate those areas of
weaknesses.
(iii) concepts should be well explained and demonstrated to the candidates.
Question 1
(a) In a class of 70 students , 40 belong to the Red Cross Society, 27 belong to the Girls' Guide Society and 12 belong to both the Red Cross Society and the
Girls Guide Society.
The remaining students do not belong to any of the two societies.
(i) illustrate the information on a Venn diagram.
(ii) How many students belong to the Red Cross Society only?
(iii) How many students do not belong to any of the two societies?
(b) A farmer uses 1/3 of his land to plant cassava, 2/5 of the remaining land to plant maize and the rest vegetables. If vegetables cover an area of 10 acres, what is the total area of the farmer's land.
Most of the candidates were able to draw a Venn diagram of two intersecting sets and labelled them correctly, while others could not illustrate the information properly on the Venn diagram. Instead of U (70), R (40) etc., they wrote U = 70, R = 40, etc.
Few candidates were able to solve the related question a (ii) whereas for (a) (iii) most of the candidates could not answer it correctly because they could not identify the part of the set which represented ''those who do not belong to the two societies''.
The part (b) of the question was quite challenging and for that matter most candidates were not able to determine that portion of land that was allocated to maize and subsequently to vegetables. It was observed that most candidates could not analyze the question to come out with the appropriate mathematical statement that will enable them to solve the question. It was realized that instead of finding 2/5 of the remaining land to plant maize,
i.e. 2/5 x 2/3 most of them added 2/5 to 1/3 i.e 2/5 + 1/3 which was wrong.
Question 2
(a) Solve for x, if 2 – 2/5x ≤ 1 1/3
(a) At a rally attended by 520 people , 30% were Fantes, 25% Nzemas, 20% Gas and the rest Gonjas.
(i) How many Gonjas were at the rally?
(ii) How many more Fantes than Nzemas were at the rally.
(iii) Draw a pie chart to illustrate the information.
This part was quite easily answered by most candidates. They converted the mixed number into improper fraction and cleared the fraction to solve the inequality.
Most of them however left the final answer as x ≥ 10/9 instead of x ≥ 1 1/9
Question 3
(a) Mr. Mensah's farm is about 20km from the house. He uses his car to travel y km of the distance from his house and then walks 1 ½ hours at the rate of 3 km per hour to get to his farm.
(a) The perimeter of a square field is the same as that of a rectangular field. If the length of the rectangular field is 8 km and width is 5 km, calculate the area of the square field.
(b) Find the gradient of the line which passes through the points M (2,-1) and K (-3,6)
(a) In the part (a) of the question most of the candidates could not answer it correctly. Even though most of them realized that y + distance on foot = 20, they were unable to determine the distance on foot giving time and the rate in km per hour.
(b) Most of the candidates demonstrated mastery in solving the plane geometry question involving rectangle and square. With the given information most candidates calculated the dimensions of the square but unfortunately in finding the area of the square most of them did not show any working.
(c) Part (c) was quite easily answered by most candidates. They showed mastery in finding the gradient of a line joining two given points. However, few candidates inverted the formula for finding the gradient as (x1-x2) / (y1-y2)
Question 4
(a) Using a ruler and a pair of compasses only, construct triangle PST with angle PST = 30°, |ST| = 9cm and |PS|= 12cm.
(b) With T as centre, draw a circle of radius 6 cm.
(c) Construct the perpendicular bisector (mediator) of line PS.
(d) Label the intersections of the circle and the mediator Q1 and Q2.
(e) (i) Measure |Q1Q2|
(ii) Measure angle Q1 T Q2.
The question was answered by most of the candidates, but unfortunately they could not exhibit all the requisite skills to construct the expected triangle PST. In constructing angle 30° most of the candidates could not bisect angle 60°.
However, some of them showed mastery in constructing triangle PST and then went ahead to locate its centre and drew a circle with radius 6cm. Unfortunately, most of them could not label the intersections of the circle and the mediator. Measuring the length Q1, Q2, and angle Q1TQ2 were inaccurate.
In e (ii) Q1 and Q2 were required to be used to complete triangle Q1TQ2 before measuring Q1TQ2. This step was omitted by the candidate.
Question 5
(a) Anita bought 51 tubers of yam at 3 for GH ¢ 10.00. If she sold them and made a loss of 40%, how much did she sell each tuber of yam?
(b) The volume of cylinder closed at one end is 1056 cm3. If its height is 21 cm, find its:
(i) diameter;
(ii) total surface area.
Part (a) was correctly answered. Candidates were able to find the total cost and the total selling prices of the yams. Also they calculated the selling price per tuber correctly. Some candidates used ' ¢' instead of 'GH¢' as the unit of currency.
Part (b) was done using the formula for the volume of a cylinder and equating that to the given volume from the equation. The diameter was then calculated by the candidates.
In e(ii) candidates did not read carefully the description given to the cylinder in the question.
ie ''cylinder closed at one end'' They used the total surface area formula as
TSA = 2 ∏ (h + r) which represented the total surface area of a closed cylinder i.e. a cylinder closed at both ends. This resulted in wrong answer to this question.
Question 6
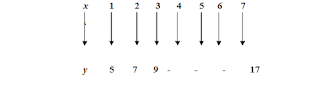
(a) (i) Copy and complete the following mapping:
(ii) Determine the rule for the mapping.
(b) Draw two perpendicular axes Ox and Oy on a graph sheet.
(c) Using a scale of 2 cm to 1 unite on the x- axis and 2cm to 2 units on the y – axis , mark the x – axis from 0 to 8 and the y – axis from 0 to 20.
(d) Plot the point for each ordered pair (x, y) and join them with a straight line.
(e) Find:
(i) y when x is 0;
(ii) x when y is 14.
(a) Most candidates copied and completed the table for the given mapping. In stating the rule for the mapping in (ii) however the candidates wrote 2x + 3 or y → 2x + 3 instead of x→ 2x +3 or y = 2x +3.
The graph of the relation was plotted using the given scale. Some candidates also failed to use the given scale. Instead of 2 cm to 1 unit the x axis, they used 2cm to 2 units,
In (e) some used the graph in (c) to find the values of y in (i) and in (ii) others used the rule in a (ii) to determine these values. This approach was accepted because the question was silent on the use of the graph to determine those values.


.webp)






No comments: