BECE 2012 Mathematics (Maths) Paper 2 Essay
BECE 2011 MATHS
MATHEMATICS
ESSAY - Paper 2
1. (a) Evaluate,
leaving the answer in standard form.
(b) An amount of GH¢4,200.00 was shared between Aba and Kwame. If Aba had 5/7 of the
amount,
(i) how much did Kwame receive?
(ii) what percentage of Aba's share did Kwame receive?
(c) Find the value of x in the diagram below.
2. (a) A car consumes a gallon of petrol for every 30 km drive. The driver of the car set out on a
journey of 420 km with 10 gallons of petrol in the fuel tank.
(i) How many more gallons of petrol will be needed to complete the journey?
(ii) Find the cost of the petrol used for the journey of 420 km if a gallon of petrol costs
GH¢5.50
journey of 420 km with 10 gallons of petrol in the fuel tank.
(i) How many more gallons of petrol will be needed to complete the journey?
(ii) Find the cost of the petrol used for the journey of 420 km if a gallon of petrol costs
GH¢5.50
(b) The average number of spectators at a football competition for the first five days was 3,144.
The attendance on the sixth day was 3,990. Find the
(i) The total attendance on the first five days
(ii) The average attendance for the 6 days
(c) The area enclosed by a square garden is 121 m2. What is the distance around the garden?
3. (a) The table below shows the number of students who scored more than 80% in the listed subjects
Subject
|
Number of students
|
Biology
Physics
Chemistry
French
Geography
History
|
26
30
32
38
24
30
|
(i) Draw a pie chart for the distribution
(ii) What is the probability that a student chosen at random from the distribution offers Chemistry?
(b) A woman bought 210 oranges for GH¢7.50. She sold all of them at 3 for 15Gp. Find the
(i) total selling price of the oranges
(ii) percentage profit
4. The marks scored by some students in a Mathematics test are as follows:
3 3 5 6 3 4 7 8 3 4
5 4 7 4 3 7 4 6 4 8
4 5 6 3 8 4 5 6 4 5
3 3 5 6 3 4 7 8 3 4
5 4 7 4 3 7 4 6 4 8
4 5 6 3 8 4 5 6 4 5
(a) Construct a frequency distribution table for the scores.
(b) Using the table, find for the distribution, the
(i) mode;
(ii) mean, correct to one decimal place
(iii) median
5. (a) (i) Find the least Common Multiple (L.C.M.) of 9, 18 and 16.
(ii) Arrange 5/9, 7/15 and 10/16 in ascending order of magnitude
(b) Using a ruler and a pair of compasses only,
(i) construct a triangle PQR with length PQ = 10 cm, angles QPR = 45° and PQR = 60°.
(ii) Construct the perpendicular bisectors of PR and RQ to meet at T.
(iii) Measure the length of TP
(i) construct a triangle PQR with length PQ = 10 cm, angles QPR = 45° and PQR = 60°.
(ii) Construct the perpendicular bisectors of PR and RQ to meet at T.
(iii) Measure the length of TP
6. (a) (i) Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular axes Ox and Oy
on a graph sheet.
(ii) Mark on the same graph sheet, the x-axis from -5 to 5 and y-axis from -6 to 6.
(iii) Plot the points P(4, 2), Q(2, 5) and R(2, 2). Join the points P, Q, R to form a triangle
PQR
(iv) Using the x-axis as a mirror line, draw the image P1Q1R1 of the triangle PQR such that
P→P1, Q→Q1, R→R1
(v) Write down the coordinates of P1, Q1 and R1.
on a graph sheet.
(ii) Mark on the same graph sheet, the x-axis from -5 to 5 and y-axis from -6 to 6.
(iii) Plot the points P(4, 2), Q(2, 5) and R(2, 2). Join the points P, Q, R to form a triangle
PQR
(iv) Using the x-axis as a mirror line, draw the image P1Q1R1 of the triangle PQR such that
P→P1, Q→Q1, R→R1
(v) Write down the coordinates of P1, Q1 and R1.
(vii) Label the vertices of triangle P2Q2R2




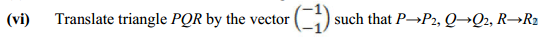
.webp)






No comments: